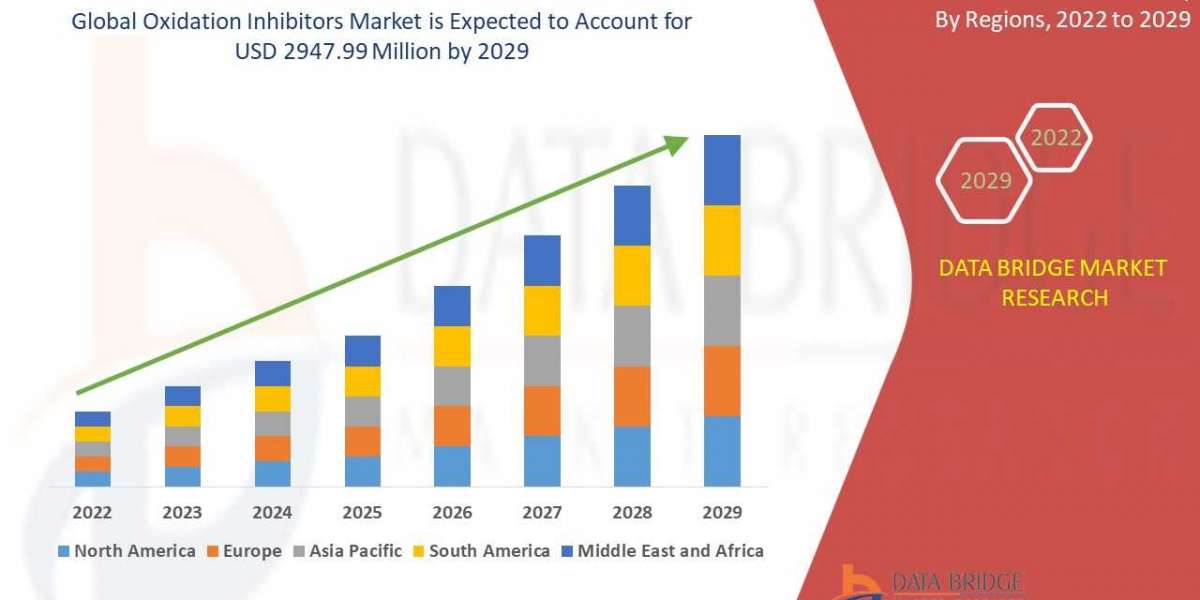
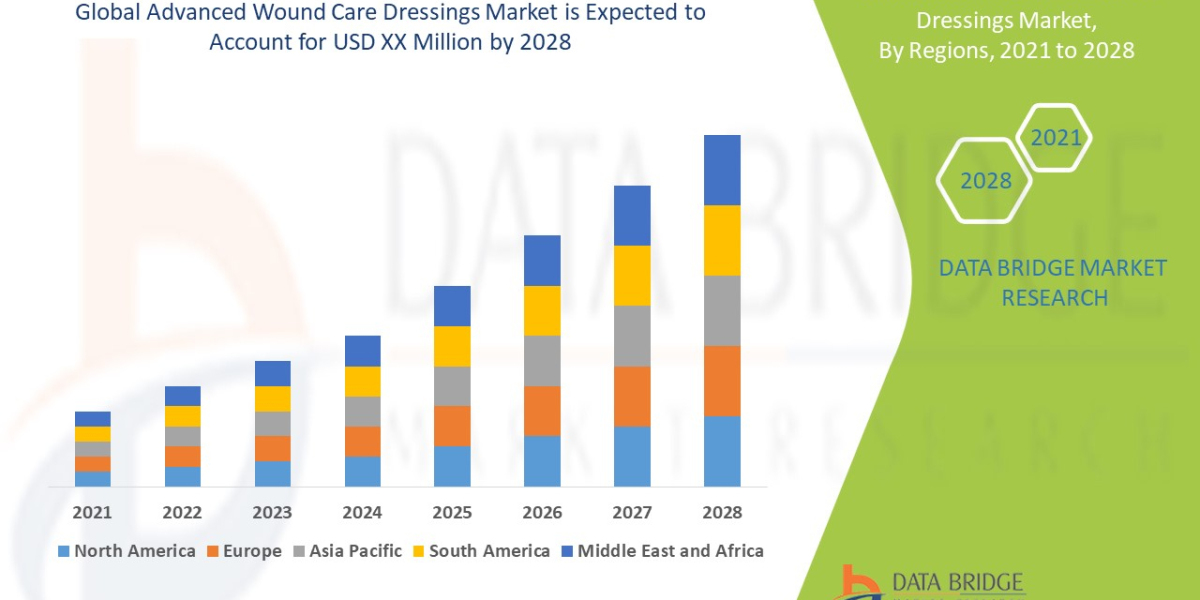
For centuries, mathematicians were fascinated by the sequence known as Fibonacci, a fascinating mathematical notion.

It is an order of values, where each value is the product of the first two numbers. The order of numbers starts at 0 or 1 and then continues endlessly.

In this article, we are going to look at the sequence known as the Fibonacci series in c, how it operates, and the best way to apply it in everyday situations.

What is The Fibonacci series?

The sequence known as Fibonacci is a series of integers in which each one is the product of two integers before it.

The order in which it starts is 0 and 1, then each successive number is product of both of the numbers following it.

As a consequence, the order of numbers will be represented as follows:

0, 1, 1, 2, 3

The Fibonacci series was given the name following Leonardo Fibonacci, who popularised it in the Western world with the publication of "Liber Abaci" in 1202. However, the series became recognised in India Arabia several years before Fibonacci.

The sequence of Fibonacci numbers is a widely recognised and fascinating mathematical series which has enthralled mathematical researchers, scientists, and artists of different age groups.

The pattern was given the name following Leonardo Fibonacci. He was a renowned Italian mathematician who first propagated it in the West with the publication of "Liber Abaci" in the year 1202.

Some of the most fascinating aspects of the sequence known as the Fibonacci series in c is how it develops in reality. The sequence can be observed in many living organisms, including cones of pine, sunflowers, and seashells.

Fibonacci sequence for example, may clarify the amount of flowers on a single bloom,the combination of foliage on a branch, and the spherical shapes on a cone of pine or seashell. Due to its connection to nature, numerous individuals think Fibonacci is more than just a theoretical wonder, but a basic component within the cosmos.

The Fibonacci series, as well as its occurring in nature, has multiple uses in science and math. It is used in financial market evaluation, encryption, and other areas as well.

If you are new to programming, you might be intrigued by the uses and the various functions that can be performed using The Fibonacci series.

If you are interested in learning how to put this sequence in use, then have a look at the next segment of the blog.

How to use The Fibonacci series?

Each of the numbers in the sequence known as Fibonacci is the product of two previous ones, pursuant to a simple formula.

The third integer in the order, for example, as 1 (0+1), the subsequent integer is 2 (1+1), and the final integer is 3 (2+1), continuing so on.

This rule produces an infinite number series that follows a specified pattern. Any subsequent numbers in the series have a ratio that equals the value known as the golden ratio, that is around 1.61803398875.

This proportion is a numerical constant found in many natural occurrences, such as spiral designs in seashells and leaf arrangements on the stem.

You can observe just a few digits to learn how the sequence operates. The first figure is nothing, and the subsequent number is one. You can put both of the initial numbers together to generate the third one in the sequence, known as 1.

The total of the following and third values equals the final value, known as 2. The total of the final and fourth values is 3, resulting in the fifth digit. And furthermore, every subsequent number corresponds to the sum of two previous digits.

The Fibonacci number system has numerous fascinating characteristics and uses throughout science, math, art, and environment.

The Fibonacci series for example, may be utilised to symbolise a rise in population and the organisation of specific plants.

In addition, the proportion of any two numbers that follow the Fibonacci series in c approaches the ratio known as the golden ratio. It is a constant in mathematics, seen in numerous natural phenomena, and used for millennia in art and architecture. It's an intriguing demonstration of how math can clarify and foresee natural events.

You can observe live demonstrations of how The Fibonacci series actually works using a C compiler. In the meanwhile, if you are interested in learning where the Fibonacci series are used in real life, then check out the following section of the blog.

What are the real-time uses of The Fibonacci series?

The Fibonacci series offers an extensive number of uses in science, math, banking, and artwork. These were a few instances of how to applythe combination of Fibonacci numbers in various scenarios:

1. Mathematics:

Many mathematical evidence and formulae employ the sequence known as Fibonacci. Fibonacci numbers, for example, exist in the Pascal triangle, a triangle-shaped collection of numbers used in combinations and probability theory.

2. Sciences:

The Fibonacci series is used in science to imitate the growth of living beings like animals and plants. The Fibonacci series is employed to explain the branching structures of plants and how to arrange flowers on the stem itself.

3. Finance:

In technical evaluation, the order of Fibonacci is used to forecast trends in the stock market. Traders utilise the retracements of Fibonacci to find possible trading opportunities. Fibonacci retracements represent levels of resistance and support based on the pattern that is reliable for trading.

4. Art:

In design and art, the order of Fibonacci is employed to create attractive designs. Based across the Fibonacci structure, the ratio of gold is a famous proportion to create balanced and lovely designs.

Winding Up

The Fibonacci series is an intriguing mathematical concept with several applications in various industries.

It is a sequence of integers whereby every value is the product of two previous numbers and maintains a precise pattern found in many natural occurrences. You can observe the functioning of The Fibonacci series using a c compiler.

The Fibonacci series can be used to approach, forecast, and produce different phenomena in science, math, finance, as well as art.

It's an excellent representation of how arithmetic is capable of clarifying and foreseeing natural processes, as well as how it may be used in practical situations.